2.2 指令格式 (con’d)
2.2.2 操作码设计 (con’d)
#重点
$\bigstar$ 设计等长拓展操作码的示例:
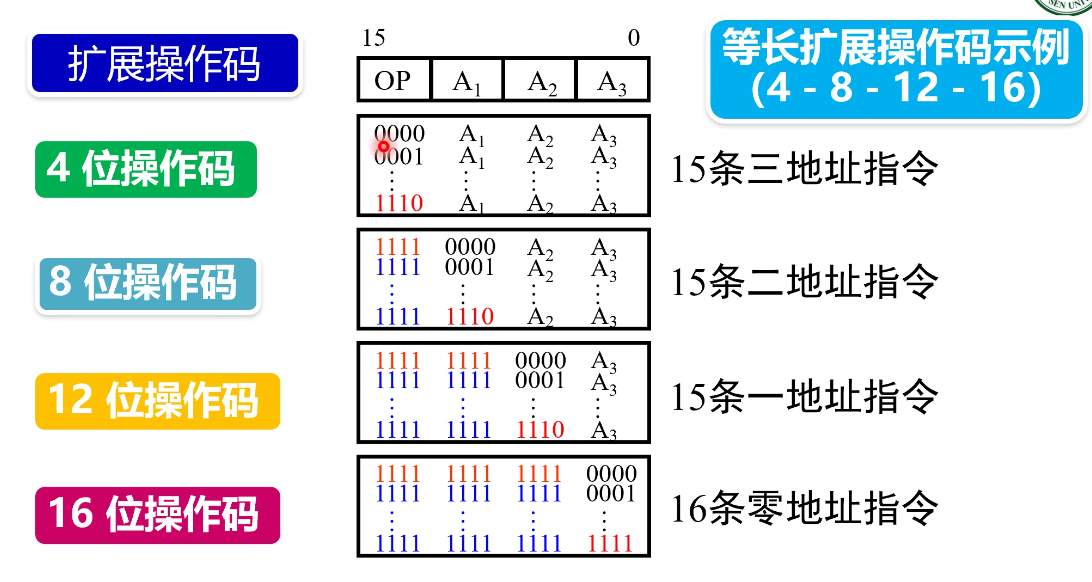
- 三地址指令:高四位 0000~1110
- 二地址指令:先用 1111 占位,然后第二个四位 0000~1110
- 一地址指令:先用 1111,1111 占位,然后第三个四位 0000~1110
- 零地址指令:先用 1111,1111,1111 占位,然后第四个四位 0000~1111
这样能够保证区分不同的指令。
拓展操作码的时候,每次需要拓展一个地址码的位域。
指令格式设计的基本原则:
- 指令尽量短
- 要有足够的操作码位数
- 指令编码必须具有唯一的解释
- 指令字长应是字节的整数倍
- 均衡设计、指令尽量规整
- 合理选择地址子段的个数
2.2.3 地址码结构
- 零地址指令
OP:无需操作数或操作数为默认 - 一地址指令
OP A1:单目运算,取反,取负,累加器 - 二地址指令
OP A1 A2:两操作数结果放到其中一个地址 - 三地址指令
OP A1 A2 A3:RISC 风格
地址字段数越多,硬件实现越复杂,程序指令数越短。
2.3 寻址方式
2.3.1 寻址方式的概念
寻址方式:寻找操作数所在位置的方法
寻址方式出现的目的:
- 扩大访问地址的范围
- 提高访问数据的灵活性和有效性
2.3.2 基本寻址方式
#重点 没法单独考,会放在大题里面模拟,可能会考非常规的寻址方式
| 寻址方式 | 解释 | 操作数/有效地址计算 | 优点 | 缺点 |
|---|---|---|---|---|
| 立即数寻址 | 直接将操作数放在指令当中 | $操作数 = A$ | - 指令执行时间短,无需访问内存 - 广泛使用 | - 操作数的大小受子段长度的限制 |
| 存储器直接寻址 | 将操作数在存储器的地址放到指令当中 | $EA = A$ | - 处理简单直接 | - 寻址空间收到指令的地址字段长度的限制 - 较少使用,在8位计算机或16位计算机 |
| 寄存器直接寻址 | 操作数在寄存器中,所在的寄存器的编号放到指令当中 | $操作数 = (R)$ | - 只需要很短的地址字段 - 无需访问内存,速度快 - 使用最多,提高性能 | - 地址范围有限 |
| 存储器间接寻址 | 指令的地址码 $A1$ 指向存储器的地址,访存得到操作数的地址 $A2$,再次访存得到操作数 $Data$ | $EA = (A)$ | - 寻址空间大,灵活,便于编程 | - 至少需要两次访存才能取到操作数 - 执行速度慢 |
| 寄存器间接寻址 | 指令的地址码 $R_n$ 指向第 $n$ 个寄存器的地址,访存得到操作数的地址 $A$,再次访存得到操作数 $Data$ | $EA = (R)$ | - 比存储器间接寻址少访问内存一次 - 寻址空间大,使用比较普遍 | 额外存储器访问 |
| 偏移寻址 | 指令的地址码 $R_b$ 指向第 $b$ 个寄存器的地址,访存得到地址 $N$,再加上立即数 $A$ 得到 $N+A$,再次访存得到操作数 $Data$ 分为相对寻址、基址寻址、变址寻址 | $EA = A + (R)$ | 灵活 | 复杂 |
| 堆栈寻址 | 堆栈是一个内存区域。 进程的区域中,栈区域从高到低地址扩展,堆区域(动态分配区)从低到高地址扩展。 堆栈指针是一个特殊寄存器,指向栈顶。 两个操作 PUSH/POP 会使指针减/加。 | $EA = SP$ | 指令短 | 应用有限 |
偏移寻址的三种类型:
跳转指令的三个重要"坑点",考试时会有具体的说明,灵活变通
$\bigstar$ PC寻址:下一条指令的地址相对于该条指令的地址码的偏移量。立即数 $A$ 代表跳过了多少条指令,他是一个有符号数。
- 起跳点是当前指令的下一条指令
- 偏移量指的是跳过的指令数而不是字节数,一般每条指令有 2字节。
- 因此目标地址就是 $PC + (1 + \Delta) \times bytes_per_instrc$
- 偏移量是一个有符号数,例如 8 位就是 $[-128, 127]$
常用于函数内部的分支、跳转指令
基址寻址:程序的头部地址放在基址寄存器当中,这个地址由操作系统确定,在程序执行过程中不会随意改变。
将文件基地址加上偏移量就得到相应函数的地址。
常用于函数之间的跳转指令。
变址寻址:数组头部地址放在变址寄存器当中,这个地址一般由用户设定,在程序执行过程中可变。
将数组基址加上偏移量就得到相应数组元素的地址。
常用于数组等顺序结构的访问。
寻址方式的确定方式:
- 在操作码中隐含寻址方式
- 显式给出寻址方式,放在寻址方式位里。
2.3.3 复合寻址方式和寻址方式实例
- 指令数等于 $2^{操作码位数}$
- 寄存器编码位数等于 $\log_2 \text{寄存器数}$
- $\bigstar$ 存储地址寄存器 $MAR$ 的位数等于 $\log_2 \text{不同的地址数} = \log_2 \frac{\text{主存地址空间大小 (byte)}}{字长 (byte)}$
- 存储数据寄存器 $MDR$ 的位数等于字长位数。