2.5 程序的机器级表示 (con’d)
2.5.1 MIPS 指令系统介绍 (con’d)
2. 寻址方式
MIPS32 体系结构中有 32 个寄存器,每个寄存器有不同的用途,二进制表示是 5 位。
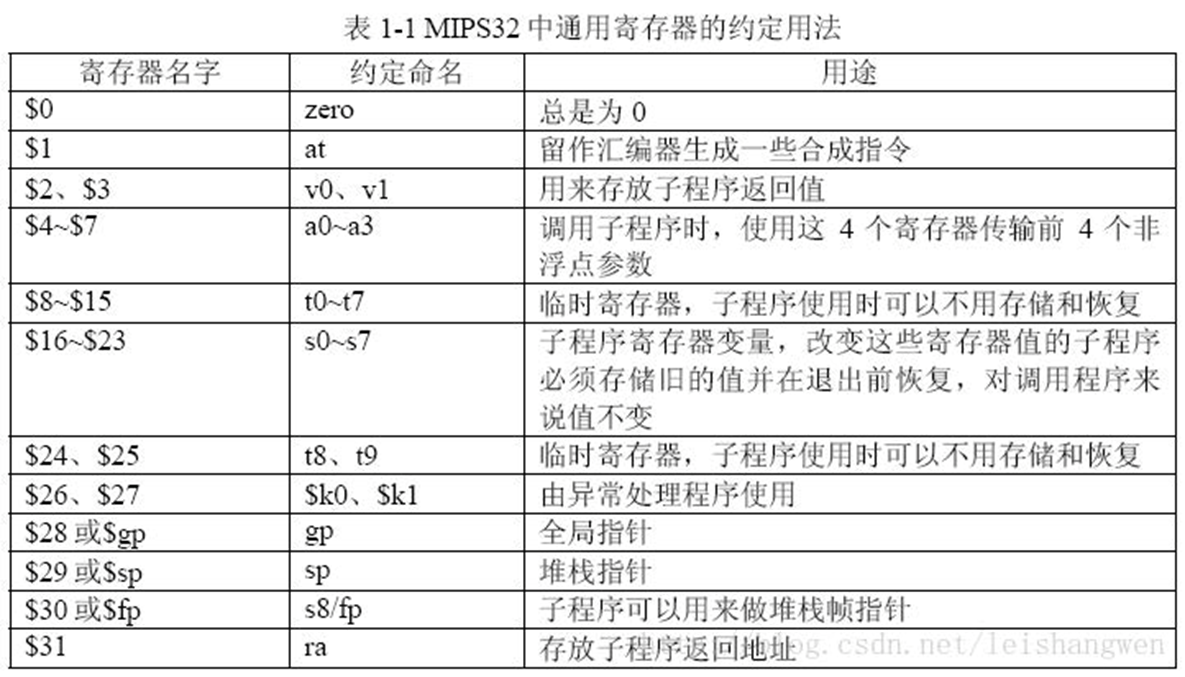
3. 指令中的操作数
分为三种:
- 寄存器数据指定:
- 32×32-bit FP Regs (f0 - f31, paired DP)
- HI、LO、PC:特殊寄存器
- 存储器数据指定:
- 只能通过Load/Store指令访问存储器数据
- 字节编址,数据要求按边界对齐
- Big Endian (大端方式)
- 可访问空间: 232bytes=4GB
- 访存地址通过一个32位寄存器内容加16位偏移量得到, 16位偏移量为有符号整数
- 立即数 / 文本 / 位
4. MIPS 指令类型
分为四种:
- 算术逻辑运算指令:
add, sub, multiply, divide, and, or, xor,…. - 数据传输指令:
load, store - 条件分支指令:
- 相等 / 不相等跳转:
beq,bne - 小于 / 大于判断:
blt,bgt,ble,bge(有对应汇编指令,无对应机器指令) - 比较结果由
slt,slti产生
- 相等 / 不相等跳转:
- 无条件跳转指令:
j label:直接跳转到目标地址jal label:跳转到子程序,并保存返回地址到$rajr rs:跳转到寄存器指定地址(一般用来返回)
条件分支指令中经常通过标志位来进行转移,常用的标志位有:
SF:NegativeVF(OF):Overflow Flag(溢出标志)- 表示有符号数的运算结果是否超出范围
- 如果有符号加法溢出(同号相加结果异号),则设为
1,否则为0 - 如果有符号减法溢出(异号相减,结果符号不对),则设为
1,否则为0
CF:Carry Flag(进位标志)- 表示无符号数的运算结果是否超出范围
- 如果无符号加法产生进位,则设为
1,否则为0 - 如果无符号减法产生借位,则设为
1,否则为0
ZR:Zero Flag
用栈为函数调用分配空间
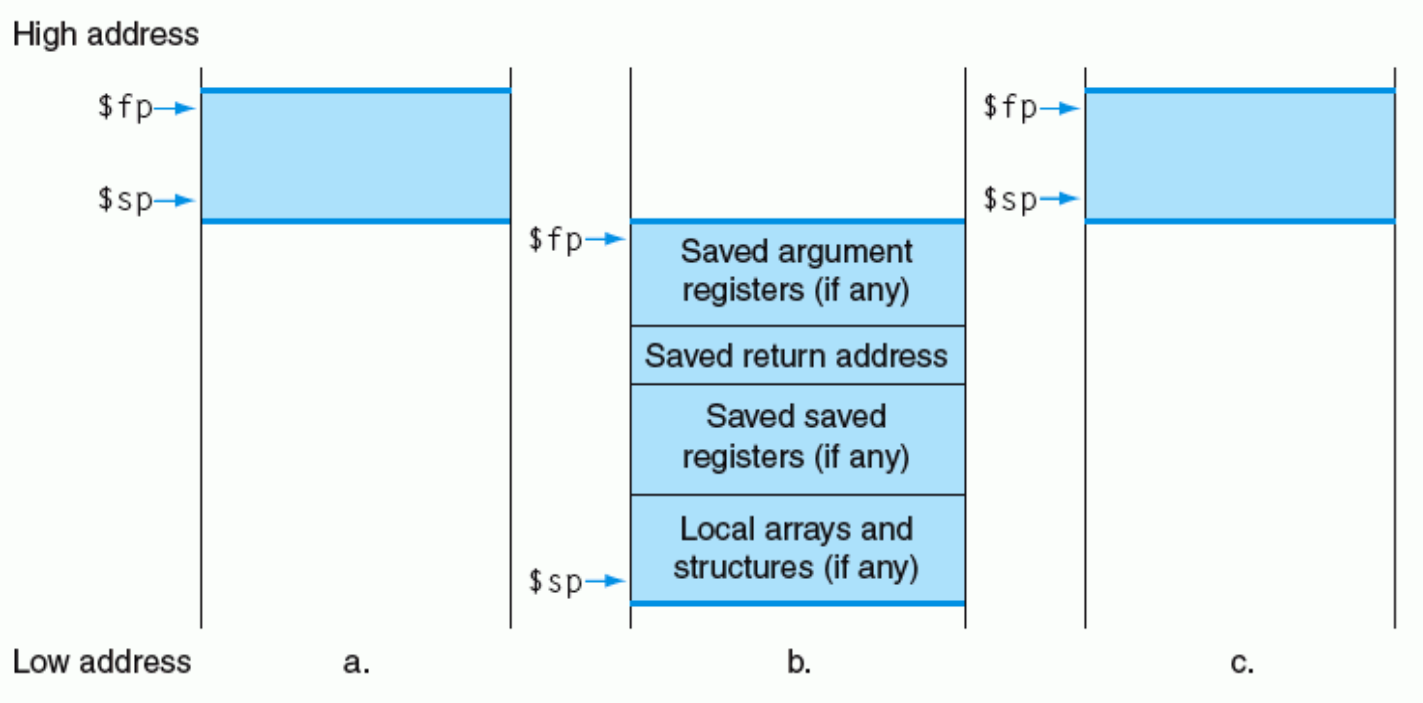
分配空间用栈实现。用帧指针 $fp 来保存子函数的寄存器地址。
在调用某个子函数的时候,首先更新 $fp,然后紧接着保存参数(从后往前)
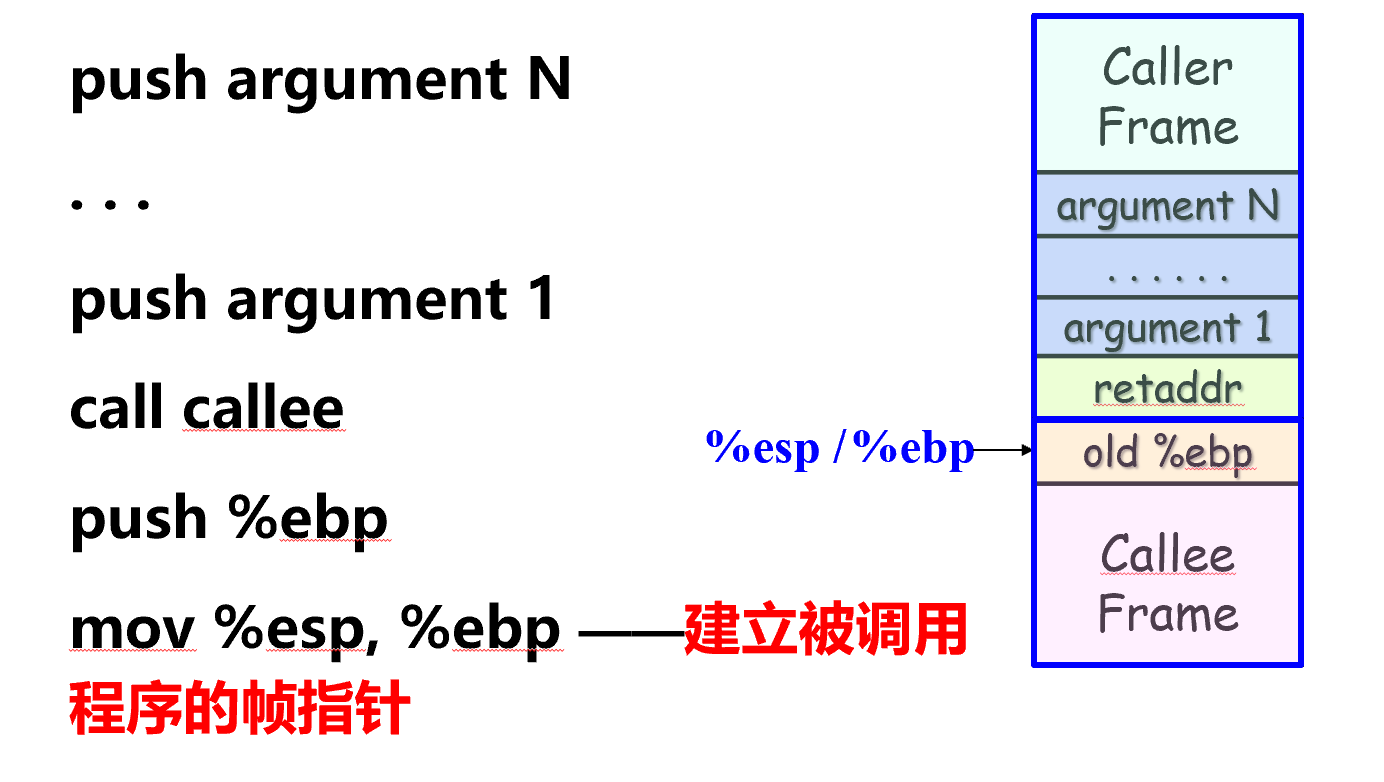
call callee:压完参数后,最后将返回地址压入栈内。这时调用程序的任务完成,决定权从调用程序给了被调用程序。
push %ebp:保存旧的帧指针(为了返回时将帧指针返回回来)
MIPS 内存布局
MIPS 的 32 位地址空间从 0x00000000 到 0xFFFFFFFF
| 区域 | 功能 | 地址范围(典型值) | 特点 |
|---|---|---|---|
| Reserved | 保留区 / 操作系统内核空间 | 0x0000_0000 ~ 0x0040_0000 | 不能被用户程序访问 |
| Text Segment | 程序代码段(指令) | 0x0040_0000 ~ 0x1000_0000 | 存放可执行指令 |
| Static Data Segment | 静态数据区(全局变量) | 0x1000_0000 ~ 0x1001_0000 | 程序运行前就分配好 |
| Dynamic Data Segment (Heap) | 动态数据区(堆) | 0x1001_0000 ~ 向高地址增长 | 用于 malloc 或动态分配 |
| Stack Segment | 栈区 | 从高地址 0x7FFF_FFFC 向低地址增长 | 用于函数调用、局部变量 |
| Kernel space | 内核代码 / 数据 | 0x8000_0000 以上 | 用户态不可访问 |
0x0000_0000 ─► Reserved(保留)
0x0040_0000 ─► Text(代码) ← $pc
0x1000_0000 ─► Static Data(静态数据)
0x1000_8000 ─► $gp
↑
│ Dynamic data (heap)
↓
0x7FFF_FFFC ─► Stack(栈顶) ← $sp
- 静态数据区(Static Data)大约在
0x1000_0000 ~ 0x1000_FFFF。 $gp取其中间值(0x1000_8000)方便前后各 32KB 偏移访问。
程序的翻译和启动执行
Complier, Assembler, Linker, Loader
3.1 概述:基本运算
3.1.1 按位运算
按位与 &:用于提取二进制数中的指定位。
按位或 |:用于特定位上的无条件赋值。
按位取反 ~:将所有位取反
按位异或 ^:将特定位取反,或者实现两数按位的比较
3.1.2 逻辑运算
逻辑与 &&、逻辑或 ||、逻辑非 !
按位运算结果是一个 01 串,逻辑运算结果是一个逻辑值。
3.1.3 移位运算
| 运算类型 | 功能 | 最高位 | 最低位 | 移位操作 | 溢出判断 |
|---|---|---|---|---|---|
| 算术左移 / 补码左移 | 向高位移动特定位数 | 移出 | 补 0 | [signed] << k | 若移出的位不等于新的符号位即 $CF \oplus SF = 1$,则溢出 |
| 逻辑左移 | 向高位移动特定位数 | 移出 | 补 0 | [unsigned] << k | 高位移出了 1 |
| 算术右移 / 补码右移 | 向低位移动特定位数 | 补原符号位 | 移出 | [signed] >> k | 不溢出但可能数据丢失 |
| 逻辑右移 | 向低位移动特定位数 | 补 0 | 移出 | [unsigned] >> k | 不溢出但可能数据丢失 |
算术右移对于负数补码,得到的结果会向负无穷取整而不是向零取整。
如 -3 (11111101) 算术右移 1 位得到 -2 (11111110) 而不是 -1.
移位运算既可以看作是数学意义上的运算(算术运算),也可以看作是位上的逻辑操作(逻辑运算)
C 语言中的基本运算
位扩展和位截断:发生在强制类型转换时。
| 操作类型 | 操作数 | 操作形式 | 风险 |
|---|---|---|---|
| 位扩展 | 无符号数 | 高位补 0 | |
| 位扩展 | 有符号数 | 高位补原符号位 | |
| 位截断 | 直接截去高位 | 可能会发生数据溢出 |
有符号数和无符号数加入寄存器的时候,有符号数需要用符号位填充高位(符号扩展),无符号数需要用 0 填充高位(0 扩展)
3.2 加法和减法
原码二进制加法
原则:符号位和数值位分别处理
同号相加:数值位相加,符号位不变。若最高位进位则溢出。
异号相加:负数取补码与正数相加。此时必然不会溢出。
- 若最高位产生进位,则结果为正数。
- 若最高位没有产生进位,则结果为负数的补码,需要再求补得到结果。
- 原理:对于数值位 $A, B$,其中 $B$ 符号位为
1。我们有 $B + [B]_补 = 2^{n + 1}$,那么 $A + [B]补 = A - B + 2^{n + 1}$,因此如果有进位就是准确的,没有进位就是形成了 $[B - A]{补} = 2^{n + 1} - [B - A]$ 的形式,需要求补后才能得到准确的值。
移码加减运算
移码的加减法:

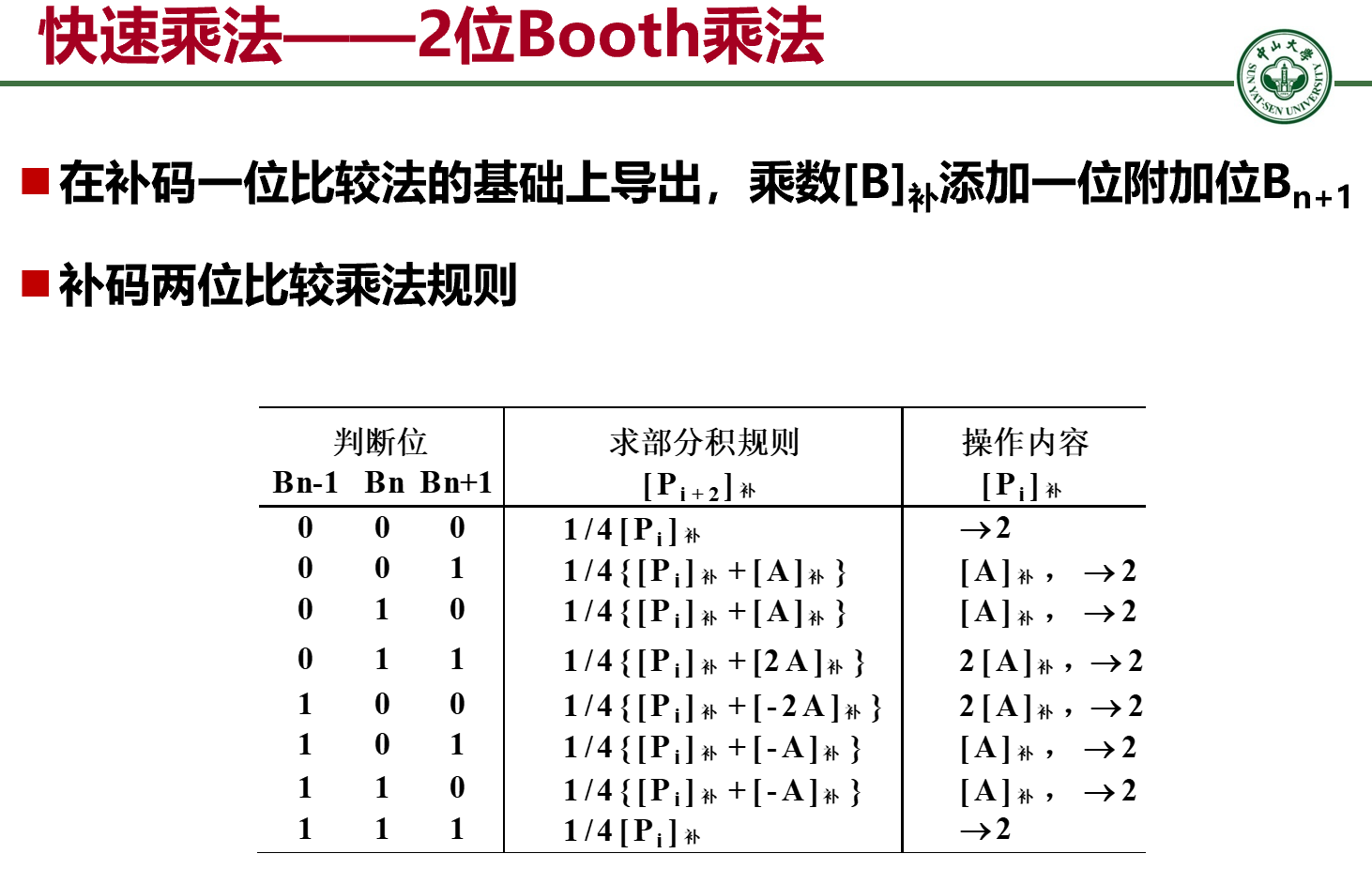
3.3 乘法和除法
补码一位乘法
对于 $C = A \times B$,其中 $A, B$ 是定点小数,被乘数采用两位符号位 $A_{01} A_{02}$,乘数的采用一位符号位 $B_0$.
被乘数采用模四补码 $[A] = 2^2 + A \pmod 4$,乘数采用一位补码 $[B] = 2 + B \pmod 2$.
若 $A<0$,则 $[A] = 11.A_0^\sim A_1^\sim A_2^\sim \cdots$,若 $A > 0$,则 $[A] = 00.A_0A_1A_2\cdots$
若 $B<0$,则 $[B] = 1.B_0^\sim B_1^\sim B_2^\sim \cdots$,若 $B > 0$,则 $[B] = 0.A_0A_1A_2\cdots$
| $A$ | $B$ | $[A]\times[B]$ |
|---|---|---|
| $A \ge 0$ | $B \ge 0$ | $[A] = A, [B] = B$ |
| $A < 0$ | $B \ge 0$ | $[A] \equiv 2^{2} + A \equiv 2^{n + 2} + A \pmod 4$ $[A]\times [B] \equiv [A] \times B \equiv (2^{n+2}+A)B \equiv 2^2 + AB = [AB]\pmod 4$ 其中 $2^{n+2}B$ 是 $4$ 的倍数,可约去 |
| $B < 0$ | $B = [B] - 2 = 0.B_1^~B_2^ $\begin{aligned}\ [AB] &= [A(0.B_1^~B_2^ | |
| $[AB] = [A] \times [B]_{mantissa} + [-A] \times B_0$ |


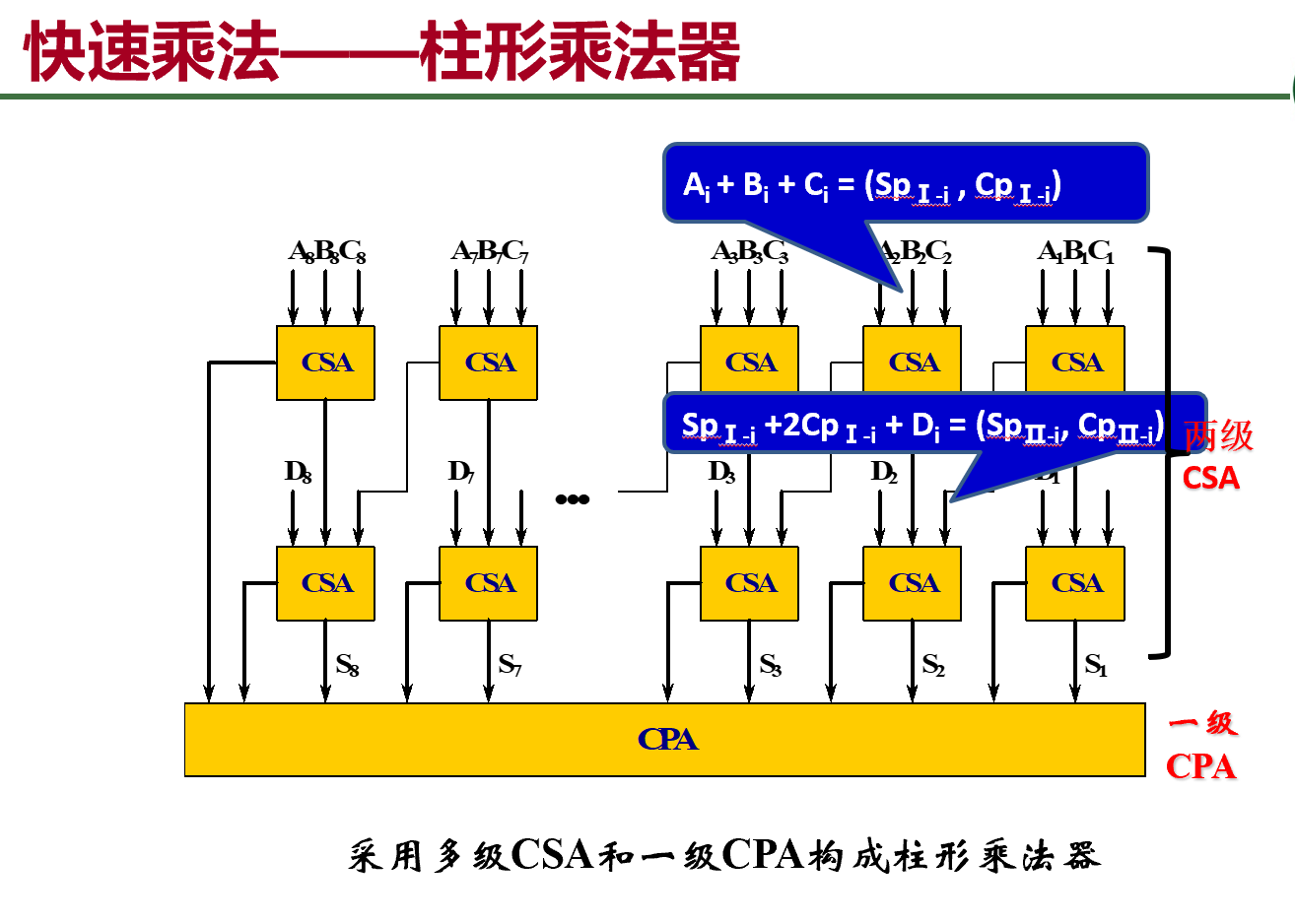
3.4 除法运算
3.5 浮点数运算
#重点 浮点数加减法(阶码对齐,注意溢出的问题)