重点内容:
IEEE 754 单精度浮点数
大小端、对齐问题
有符号数、无符号数、四种标志位
浮点数加减法
2.1 数制与编码
进制转换、BCD码、定点数编码、整数表示
进制转换略。注意点:十进制的有限小数在二进制中不一定就是有限小数,但是任意二进制有限小数在十进制中都是有限小数。
真值:数学里的实际值
机器数:对真值的编码得到的二进制序列,如原码、反码、补码。
浮点数在计算机的两种数据格式:定点表示、浮点表示。
常用 定点补码整数 表示整数,浮点小数 表示浮点数。
| 数的类型 | 码的类型 | 定义 |
|---|---|---|
| 纯小数 | 原码 | $$[x]_原 = \begin{cases} x, & 0 \le x < 1 \\ 1 + \lvert x\rvert,& -1 < x \le 0\end{cases}$$ |
| 纯整数 | 原码 ($n$ 位) | $$[x]_原 = \begin{cases} x, & 0 \le x < 2^{n - 1} \\ 2^{n - 1} + \lvert x \rvert,& -2^{n - 1} < x \le 0\end{cases}$$ |
| 纯小数 | 补码 | $$[x]_补 = \begin{cases} x, & 0 \le x < 1 \\ 2 - \lvert x\rvert,& -1 \le x < 0\end{cases}$$ |
| 纯整数 | 补码 ($n$ 位) | $$[x]_补 = \begin{cases} x, & 0 \le x < 2^{n - 1} \\ 2^n - \lvert x \rvert,& -2^{n - 1} \le x < 0\end{cases}$$ |
| 纯小数 | 变形补码 / 模四补码 | $$[x]_补 = \begin{cases} x, & 0 \le x < 1 \\ 4 - \lvert x\rvert,& -1 \le x < 0\end{cases}$$ 该补码中有双符号位,$00$ 表示正,$11$ 表示负 |
| 纯整数 | 移码 ($n$ 位) | $$[x]_移 = 2^n + x,\quad -2^{n - 1} \le x < 2^n$$ |
- 真值与补码之间的转换:
- 对于正数,$[x]_补 = x$;
- 对于负数(符号位为 $1$),先取反再末位 $+1$
- 补码与移码之间的转换:只需将符号位取反即可。
- 原码会存在 $[+0]_原 = 00000000,\ [-0]_原 = 10000000\ (n = 8)$,而补码只有 $[0]_补 = 00000000$,移码只有 $[0]_移 = 10000000$
- 对于补码,如果是负数,补码数值部分越大,真值越大(越靠近 $0$)
表示范围:
- 无符号整数:只有数值位,没有符号位,表示范围为 $[0, 2^n - 1]$.
- 带符号整数:通常使用补码表示,因为 $0$ 的表示唯一,符号位可以和数值位一起运算,比其他编码可以多表示 $-2^{n - 1}$,表示范围为 $[-2^{n-1}, 2^{n} - 1]$.
2.2 运算方法和运算电路
运算部件、移位运算、加减乘除运算、类型转换、数据存储方式
2.2.1 基本运算部件
运算器(ALU)的基本功能:加减乘除、与或非异或、移位、求补等等。
- 一位全加器(FA):
- 和表达式 $S_i = A_i \oplus B-i \oplus C_{i - 1}$
- 进位表达式:$C_i = A_iB_i + (A_i \oplus B_i) C_{i - 1}$,即进位的生成和延伸。
- 串行进位加法器:$n$ 个全加器串行相连可以得到 $n$ 位加法器,其计算延迟由进位信号的传递时间确定。
- 并行进位加法器:这是数电内容…

- 带标志加法器:对于有符号整数,需要一些标志信息: $$\bigstar \mathbf{IMPORTANT}\bigstar$$
| 标志名 | 场景 | 含义 | 计算方法 |
|---|---|---|---|
| CF(Carry Flag)进位标志 | 无符号数 | 加法进位 / 减法借位 | $$CF = C_n$$ |
| ZF(Zero Flag)零标志 | 结果所有位都是 $0$ | $$ZF = \lnot(F_0 \lor F_1 \lor \cdots \lor F_{n - 1})$$ | |
| SF(Sign Flag)符号标志 | 有符号数 | 结果的符号位 | $$SF = F_{n- 1}$$ |
| OF(Overflow Flag)溢出标志 | 有符号数 | 有符号数是否发生溢出:同号相加,结果变号 | $$OF = F_n \oplus F_{n - 1}$$ |
常见的判断信号举例:
- 无符号比较(只看 $CF/ZF$):
- 无符号小于:减法有借位 $CF = 1$
- 无符号大于等于:减法无借位,且结果不为零 $CF = 0 \land ZF = 0$
- 有符号比较(看 $SF/OF/ZF$):
- 有符号小于:减法溢出 $SF \oplus OF = 1$
- 有符号大于:减法无溢出,且结果不为零 $(SF \oplus OF = 0) \land (ZF = 0)$
- 结果判断(看 $SF / ZF$):
- 结果为正数:符号位为零,且总体不为零 $SF = 0 \land ZF = 0$
- 结果为负数:符号位为 $1$,$SF = 1$
- 无符号比较(只看 $CF/ZF$):
算术逻辑单元(ALU):ALU 的核心是带标志加法器,其中
ALUOp是操作控制端,其位数决定了操作的种类,$操作种类数 = 2^{ALUOp位数}$.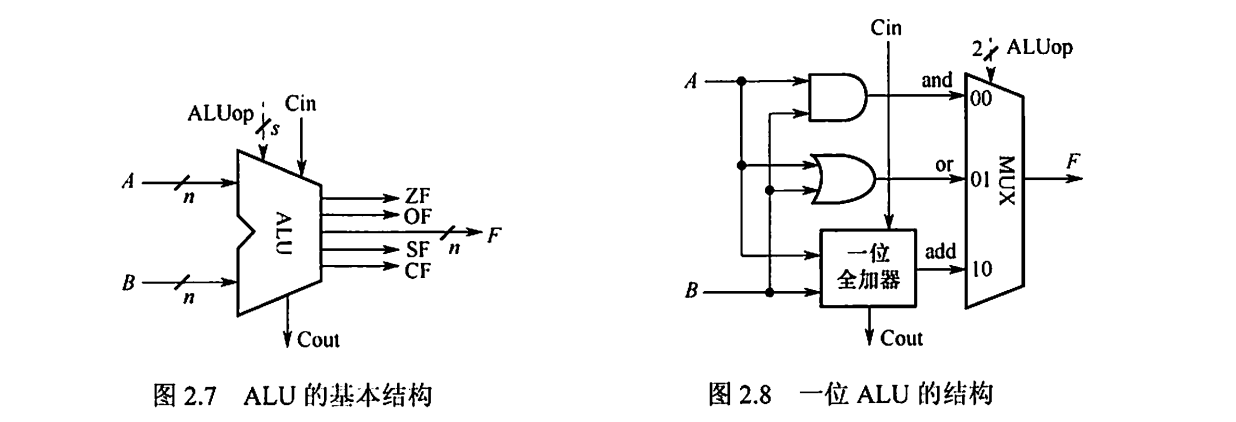
2.2.2 定点数的移位运算
下面只讨论补码: $$\bigstar \mathbf{IMPORTANT}\bigstar$$
| 移位方式 | 对象 | 移动方向 | 方法 |
|---|---|---|---|
| 算术移位 | 有符号正数 | 左/右移 | 空位补 $0$ |
| 算术移位 | 有符号负数 | 左移 | 符号位不变,空位补 $0$ |
| 算术移位 | 有符号负数 | 右移 | 符号位不变,空位补 $1$ |
| 逻辑移位 | 无符号数 | 左/右移 | 空位补 $0$ |
| 循环移位 | 左/右移 | 空位补被移出的数字 |
2.2.3+2.2.4 定点数的四则运算
- 加减法运算:用补码运算,注意溢出标志分无符号(CF)和有符号(OF)。
- 乘法:补码一位乘法(Booth 算法)
- 除法:不恢复余数法、补码除法运算(加减交替法) (这里不做重点,所以写得较简略)
2.2.5 C 语言中的整数类型及类型转换
| 类型 | 位数 | 需要记住的幂值 |
|---|---|---|
char | 1 byte,8 bit | $2^8 = 256$,$2^7 = 128$ |
short | 2 byte,16 bit | $2^{16} = 65536$,$2^{15} = 32768$ |
int | 4 byte,32 bit | |
long long | 8 byte,64 bit |
- 当
unsigned和signed之间进制转换时,数值不变,但是会改变解释这些位的方式 - 不同字长整数之间转换时:
- 大字长变量向小字长变量进行转换:高位直接截断,低位直接赋值
- 小字长变量向大字长变量进行转换:
- 若原数字是无符号整数,则进行零扩展,高位全部补 $0$
- 若原数字是有符号整数,则进行符号扩展,高位全部补原数字符号位。
2.2.6 数据的存储和排列
最低有效字节(LSB):编码的低位
最高有效字节(MSB):编码的高位
字节编址:现代计算机都是如此,每个地址编号存放一个字节。 $$\bigstar \mathbf{IMPORTANT}\bigstar$$ 大端方式(big endian):最高有效字节放在地址较小的地方
小端方式(little endian):最低有效字节放在地址较小的地方
下图是对 01 23 45 67H 的存储示例:
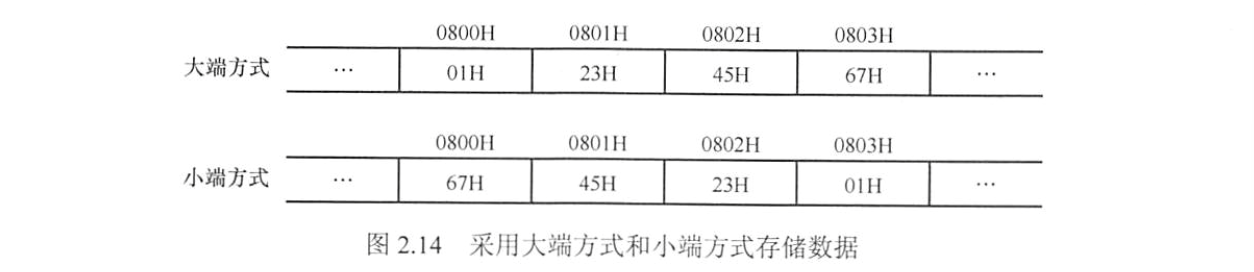
在阅读小端方式的机器代码时,字节是以相反顺序显示的。 $$\bigstar \mathbf{IMPORTANT}\bigstar$$ 数据对齐:假设字的宽度为 32 位(4 字节),按字节编址,那么
- 双字地址(如
double8 字节):首地址放在 8 的倍数 - 字地址(如
int4 字节):首地址放在 4 的倍数 - 半字地址(如
short2 字节):首地址放在 2 的倍数 - 字节地址(如
double1 字节):地址可随意 - 这样可以提高取指和取数的速度,但会造成一定的空间浪费。
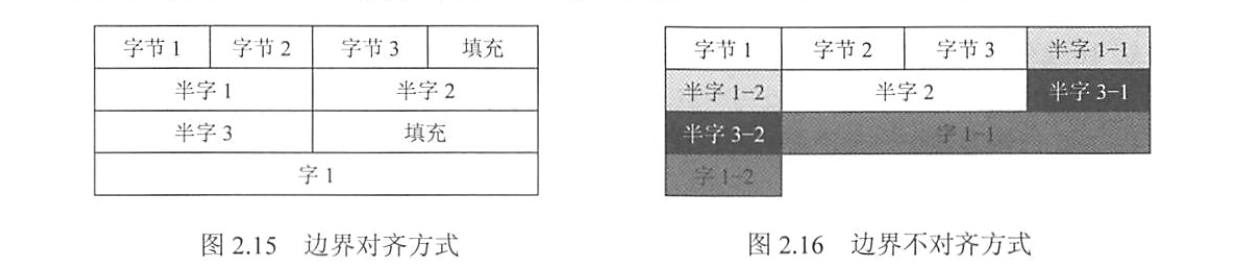
2.3 浮点数的表示与运算
浮点数的表示、加减运算
2.3.1 浮点数的表示
浮点数的表示格式:$N = (-1)^S \times M \times 2^E$
- $S$:Sign,数符
- $M$:Mantissa,尾数
- $E$:Exponent,阶码,用移码表示

浮点数的表示范围: 数据上溢时,出现异常,进行溢出处理。
数据下溢时,浮点数值趋于零,计算机将其当做机器零处理。
数据上溢时,出现异常,进行溢出处理。
数据下溢时,浮点数值趋于零,计算机将其当做机器零处理。
浮点数的规格化:
- 左规:当尾数绝对值 $<1$,则需要重复地尾数左移一位,阶码减一。
- 右规:当尾数绝对值 $\ge 2$,则需要重复地尾数右移一位,阶码加一。
IEEE 754 单精度浮点数标准: $$\bigstar \mathbf{IMPORTANT}\bigstar$$
- 数符 $S$ 有 $1$ 位,阶码 $E$ 有 $8$ 位,尾数 $M$ 有 $23$ 位,总共 $32$ 位。
- 阶码的偏置值为 $7FH = (127)_{10}$
- 尾数的数值最高位总是整数部分的 $1$,而将其隐藏,因此一共有 $24$ 位有效数字。
| 符号位 S | 阶码 E | 尾数 M | 数据类型 | 真值 | 最大值 | 最小值 |
|---|---|---|---|---|---|---|
| $0 / 1$ | $1\sim 254$ | 任意 | 规格化数 | $\displaystyle (-1)^S \times (1.M)_2 \times 2^{E-127}$ | $(2 - 2^{-23}) \times 2^{127}$ | $1.0 \times 2^{-126}$ |
| $0 / 1$ | 全 $0$ | 非 $0$ | 非规格化数 | $\displaystyle (-1)^S \times (0.M)_2 \times 2^{-126}$ | $(1 - 2^{-23}) \times 2^{-126}$ | $2^{-149}$ |
| $0 / 1$ | 全 $0$ | $0$ | $\pm 0$ | $\pm0$ | $0$ | $0$ |
| $0 / 1$ | 全 $1$ | $0$ | $\pm \infty$ | $\pm\infty$ | — | — |
| $0 / 1$ | 全 $1$ | 非 $0$ | $NaN$ | $NaN$ | — | — |
2.3.2 浮点数的加减运算
$$\bigstar \mathbf{IMPORTANT}\bigstar$$ 浮点数加减运算的步骤:
- 对阶:使两个数的阶码相等。小阶向大阶看齐,每次将阶码小的数进行右规(尾数右移一位,阶码加一)。其中可能会舍弃掉有效位,产生误差。
- 尾数运算:对尾数进行加减法。
- 规格化:结果不一定是规格化的,需要规格化处理,进行左规/右规。
- 舍入:在对阶和最终规格化的时候,可能会对位数进行右移。此时,需要保留低位移出的两位。方法有 0 舍 1 入法(常用)、恒置 1 法、截断法。
- 溢出判断:在规格化的时候,
- 尾数舍入:当数值很大的尾数舍入时,可能因为末位加 $1$ 而产生尾数移出,需要进一步右规来调整尾数和阶数 (可调整,所以还不算真正的移出)
- 右规:当阶数变为全 $1$,则会发生指数上溢
- 左规:当阶码变为全 $0$,则会发生指数下溢
C 语言中的浮点数转换:
int -> float:不会溢出,但是如果int的有效精度 $> 24$ 位,则需要舍入处理,影响精度。int/float -> double:能保留精确值double -> float:可能会溢出,或者发生舍入float/double -> int:向 $0$ 方向截断,只留下整数部分,发生舍入。并且可能会溢出。