5.1 集合的基本概念
子集:$A \subseteq B$ 当且仅当 $\forall x (x \in A \to x \in B)$
相等:$A = B$ 当且仅当 $\forall x (x \in A \leftrightarrow x \in B)$,或者 $A \subseteq B \land B \subseteq A$
真子集:$A \subseteq B \land A \ne B$
空集:$\forall x (x \in \emptyset)$
子集的性质:
- 自反性:$A \subseteq A$
- 传递性:$A \subseteq B \land B \subseteq C \to A \subseteq C$
- 空集:$\emptyset \subseteq A$
定义集合法:
| 方法 | 描述 | 例子 |
|---|---|---|
| 元素枚举法 | 将集合的所有元素一一罗列出来 | ${1, 2, 3, 4}$ |
| 性质概括法 | 用谓词概括元素满足的共同性质 基本形式:${x \mid P(x)}$,扩展形式:${f(x) \mid P(x)}$ 所有集合必须从已有集合中定义,否则产生罗素悖论 | 罗素悖论:P = ${x \mid x \notin P}$ |
| 归纳定义法 | 归纳基 + 归纳步 | $2, 6 \in S$ $x, y \in S \to x + y, x - y\in S$ |
文氏图:方框表示全集、其他封闭图形表示集合。图形的相交表示交集。
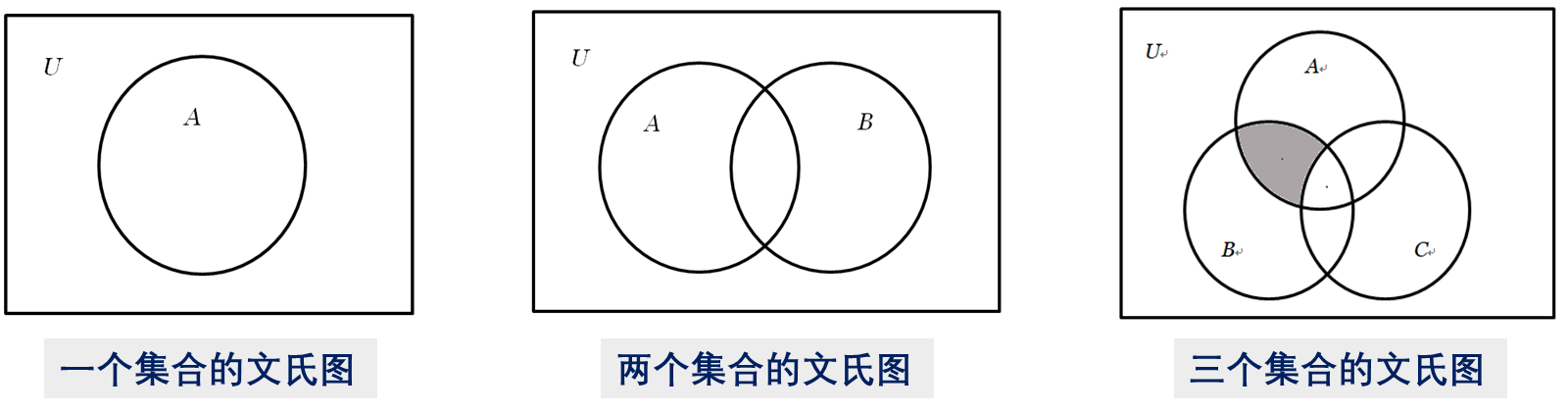
5.2 集合运算
集合并和集合交都满足交换律、结合律和幂等律
集合并对集合交有分配律,集合交对集合并也有分配律
交与子集关系:
- $A \cap B \subseteq A$, $A \cap B \subseteq B$
- $C \subseteq A \cap B \Leftrightarrow C \subseteq A \land C \subseteq B$
并与子集关系:
- $A \subseteq A \cup B$, $B \subseteq A \cup B$
- $A \cup B \subseteq C \Leftrightarrow A \subseteq C \land B \subseteq C$
差、补与子集关系:
- $A - B \subseteq A$
- $A \subseteq B \Leftrightarrow A - B = \emptyset$
- $A \subseteq B \Leftrightarrow \overline{B} \subseteq \overline{A}$
集合族:以集合为元素的集合,用花体字母表示。
广义交:对于集合族 $\mathcal A$,广义交为所有集合的交:$\cap \mathcal A = {x \mid \forall S \in \mathcal A,\ x \in S}$
广义并:对于集合族 $\mathcal A$,广义并为所有集合的并:$\cup \mathcal A = {x \mid \exists S \in \mathcal A,\ x \in S}$
幂集:所有子集构成的集合 $\wp(A) = {S \mid S \subseteq A}$
5.3 集合等式
集合等式:断言两种不同形式定义或表达的集合相等。
证明集合等式的方法:
元素考察法:考察每个元素要么都在两个集合,要么都不在两个集合。
- 基于定义:$\forall x$,从 $x \in A$ 推出 $x \in B$.
成员关系表:二进制枚举所有是否属于基本集合的各种组合,那么每一列相当于命题逻辑,可以构建出真值表。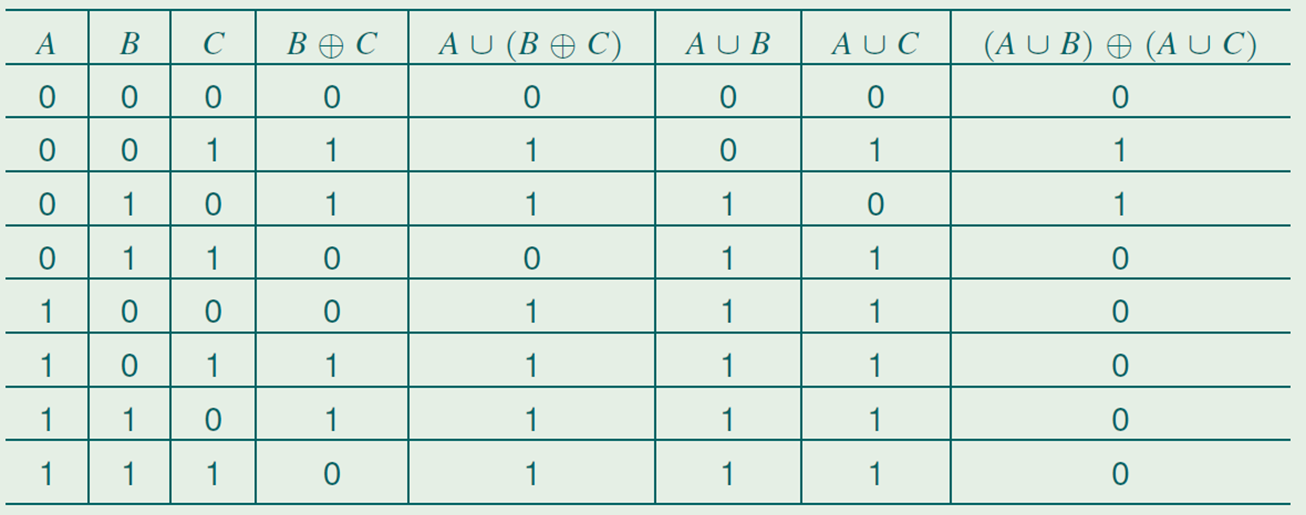
等式演算法:利用基本集合等式,演算方式证明。

重点关注:吸收律、集合差等式
子集关系法:根据集合等式与子集关系的联系证明。
- 集合交与子集关系:
- $A \cap B = A \Leftrightarrow A \subseteq B$
- $A \cap B \subseteq A$
- $C \subseteq A \cap B \Leftrightarrow C \subseteq A \land C \subseteq B$
- $A \subseteq B \land C \subseteq D \Rightarrow A \cap C \subseteq B \cap D$
- 集合并与子集关系:
- $A \cup B = A \Leftrightarrow A \subseteq B$
- $A \subseteq A \cup B$
- $A \cup B \subseteq C\Leftrightarrow A \subseteq C \land B \subseteq C$
- $A \subseteq B \land C \subseteq D \Rightarrow A \cup C \subseteq B \cup D$
- 集合差/补与子集关系:
- $A - B \subseteq A$
- $A \subseteq B \Leftrightarrow A -B =\emptyset$
- $A \subseteq B \Leftrightarrow \overline{B}\subseteq \overline{A}$
- 幂集与子集关系:
- $A \subseteq B \Rightarrow \wp(A)\subseteq\wp(B)$
#注意 #记忆 根据集合等式证明题判断方法规则:
- 单纯的集合等式证明,涉及三个集合以内,出现 $\oplus,\ \cap,\ \cup,\ -$:用成员关系表最快
- 找反例:用描述型集合,最好集合不超过两个元素来做(eg. $\emptyset,\ {1},\ {1, 2}$)
- 目标是 $\subseteq$:默认用元素考察法,常常需要分类讨论(是否属于某个集合 / 并集时讨论属于哪个集合)
- 差集 / 补集很多:把 $A - B \Rightarrow A \cap \overline{B}$,然后用等值演算
- 证明等式 / 当且仅当:拆成 $A \subseteq B,\ B \subseteq A$ 两步来证明,然后默认用元素考察法
- 前提是 $X \subseteq Y$,结论是 $Z \subseteq W$:
- 可以尝试反证法,如果存在 $x \in Z - W$,则会推出矛盾
- 可以使用子集推演
- 幂集:
- 将 $S \in \wp(A) \Rightarrow S \subseteq A$,一般是对 $S$ 作为元素考察。
- 使用 $A \subseteq B \Rightarrow \wp(A)\subseteq\wp(B)$ 来推演