概念
函数:记为 $f: A \to B \subseteq A \times B$,且满足 $\forall a \in A,\ \exists! b \in B,\ \langle a, b \rangle \in f$
- 对于每个对应关系 $\langle a, b \rangle$,记作 $b = f(a)$,称 $b$ 是 $a$ 的 像,$a$ 是 $b$ 的 原像。
- $A$ 是 $f$ 的 定义域 / 域,$B$ 是 $f$ 的 陪域。
- 像集:$f(S) = {f(x) \in B \mid x\in S}$,其中 $S \subseteq A$.
- 原像集:$f^{-1}(T) = { x \in A \mid f(x) \in T }$,其中 $T \subseteq B$.
- 值域:$f(A),\ ran(f)$.
定义方法:性质概括法、元素枚举法。
恒等函数:$id_A = \Delta_A$.
特征函数:$\chi_S(a) = \begin{cases} 1,&a \in S\0,&a \notin S\end{cases}$
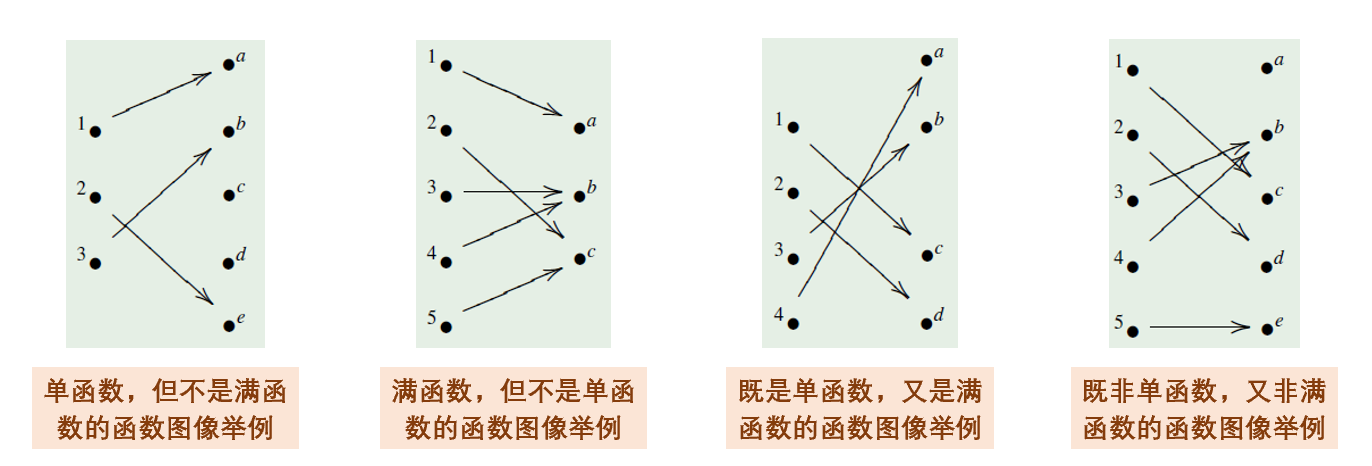
单函数 / 一对一函数:$\forall x, y \in A,\ x \ne y \Rightarrow f(x) \ne f(y)$.
满函数 / 映上函数:$ran(f) = B$.
双函数:既是单函数又是满函数。即 $\forall y \in B, \exists! x \in A,\ f(x) = y$.
运算
函数复合:等同于关系复合,$(g \circ f)(x) = g(f(x))$.
函数复合的性质:
- 单位元:对于 $f: A \to B$,有 $id_B \circ f = f = f \circ id_A$.
- 结合律:$h \circ (g \circ f) = (h \circ g) \circ f$.
- 函数复合保持函数单满性质:如 $f, g$ 都是单/满/双函数,那么 $g \circ f$ 也是单/满/双函数。
双函数的逆函数 / 反函数:对于双函数 $f: A \to B$,其逆函数为 $g: B \to A = { \langle y, x \rangle \mid \langle x, y\rangle \in f}$.
- 二者关系:$g \circ f = id_A,\ f \circ g = id_B$.
- 函数是双函数 $\Leftrightarrow$ 函数存在逆函数。
左逆函数:$g : B \to A$ 是 $f$ 的左逆,当且仅当 $g \circ f = id_A$.
右逆函数:$g : B \to A$ 是 $f$ 的右逆,当且仅当 $f \circ g = id_A$.
*基数
等势:若存在 $f: A \to B$ 是双函数,则 $A$ 和 $B$ 等势,记作 $A \approx B$.
- 性质:自反性、对称性、传递性
- 例子:$\mathbb N \approx \mathbb Z,\ \mathbb R \approx (0, 1),\ \mathcal p(A) \approx \mathbb 2^A$.
- 对于有穷集,若 $|A| = |B| \Leftrightarrow A \approx B$.
康托尔定理:对任意集合 $A$,它的幂集 $℘(A)$ 的势大于 $A$.
归纳集:$\emptyset \in A$,且若 $S \in A$,那么后继 $S^+ \in A$.
有穷集:有穷个元素的集合。
无穷集:无穷个元素的集合,判定:$\exists B \subset A,\ A \approx B$.
基数:$Card(A) = |A|$
- 对于有限集,$|A|$ 就是元素个数。
- $\mathbb N,\ \mathbb R$ 的基数为 $\aleph_0$.
- $A \approx B \Leftrightarrow |A| = |B|$.
- 施罗德-伯恩斯坦定理:既存在 $A$ 到 $B$ 的单函数又存在 $B$ 到 $A$ 的单函数,则 $A$ 与 $B$ 等势。
可数集 / 可枚举集:有穷集,或与自然数等势的集合。
- 例子:$\mathbb N$, $\mathbb Z,\ \mathbb N*$, $\mathbb Z^+\times \mathbb Z^+$, $\mathbb N^+\times \mathbb N^+$.
不可数集:比自然数势更大的集合。
- 例子:$\mathbb R,\ \mathbb N^{\mathbb N} = {f : \mathbb N \to \mathbb N}$
算法复杂度
大 O 记号:对于函数 $f, g$,若 $f \in O(g)$,那么 $\exists C > 0,\ k >0, \ \forall x > k,\ |f(x)| \le C|g(x)|$.
- 代表函数 $g$ 刻画了函数增长的一种上界。
常见函数增长情况比较(从快到慢):
- 指数函数:$b^n\ (b > 1)$.
- 幂函数:$n^c\ (c > 0)$.
- 对数函数:$(log_b n)^c\ (b > 1,\ c > 0)$.
大 O 记号的运算:
- $\max(f_1, f_2) \in O(max(g_1,g_2))$.
- $f_1 + f_2 \in O(g_1+g_2)$.
- $f_1·f_2 \in O(g_1·g_2)$.
判断算法时间复杂度,已经十分熟悉,略去。
易解问题 / P 问题:存在多项式时间复杂度的算法的问题。
不易解问题:不存在多项式时间复杂度的算法的问题。
NP 问题:能在多项式时间复杂度内检查解正确性的问题,但无法知道其是否存在多项式时间复杂度的算法(P = NP?)。
NP-Complete / NPC 问题:所有的 NP 问题可归结为该问题的问题。
P = NP?:问 NP 问题是否存在多项式时间复杂度算法。
该问题的求解困难,是因为缺乏一种能够描述算法能力边界的数学工具。
可解问题:存在算法的问题。
不可解问题:不存在有效算法的问题。
不可解问题的例子:
- 图灵停机问题:判定任意计算机程序的执行会否终止
- 一阶逻辑公式的可满足性问题
- 程序是否有死循环
- 程序是否会触发某个特定状态
- 某个命题是否由形式系统可证明
- 某些数学猜想是否可由算法判定